Stående våg: Skillnad mellan sidversioner
Ingen redigeringssammanfattning |
Ingen redigeringssammanfattning |
||
| Rad 3: | Rad 3: | ||
===Utseende=== | ===Utseende=== | ||
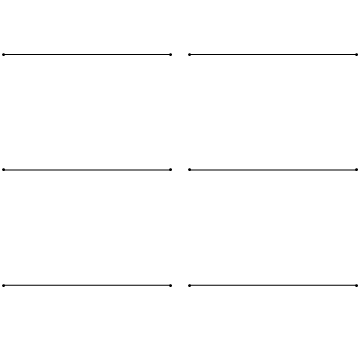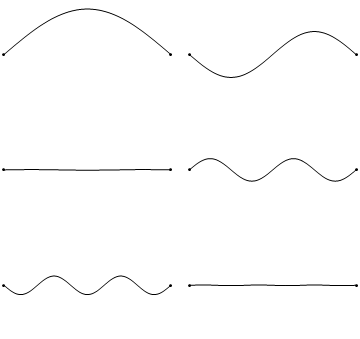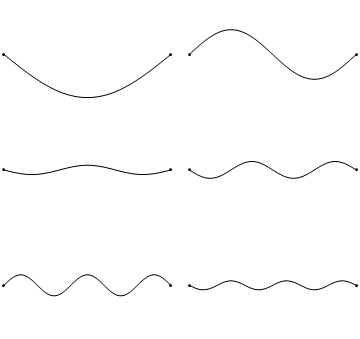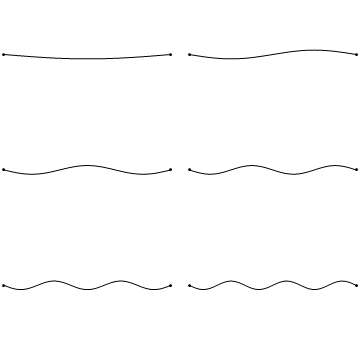
Beroende på ordningstalet på den stående vågen kommer den att ha olika antal bukar och noder, nedan visas stående vågor med ordningstalen 1 - 6. Våglängden beror på frekvensen vilket syns i bildsviten nedan; ju fler noder på strängen, desto kortare våglängd och desto högre frekvens. | Beroende på ordningstalet på den stående vågen kommer den att ha olika antal bukar och noder, nedan visas stående vågor med ordningstalen 1 - 6. Våglängden beror på frekvensen vilket syns i bildsviten nedan; ju fler [[stående våg#Noder på stående vågor|noder]] på strängen, desto kortare våglängd och desto högre frekvens. | ||
[[File:Standing_waves_on_a_string_animation.gif|frame|Stående vågor med ordningstalen 1 - 6.]] | [[File:Standing_waves_on_a_string_animation.gif|frame|Stående vågor med ordningstalen 1 - 6.]] | ||
Versionen från 1 juni 2019 kl. 17.14
Vad en stående våg är
Då två vågor möter varandra, på t ex en sträng, så ges den resulterande vågen som summan av de de båda vågornas utslag. Detta kallas för superpositionsprincipen. Under vissa sådana förhållanden skapas en stående våg. Det gäller när de båda vågornas våglängder är lika stora och då ett helt antal halva våglängder får plats på strängen. För stående vågor på en sträng gäller ofta att det är en reflekterad våg som interfererar med den inkommande vågen.
Utseende
Beroende på ordningstalet på den stående vågen kommer den att ha olika antal bukar och noder, nedan visas stående vågor med ordningstalen 1 - 6. Våglängden beror på frekvensen vilket syns i bildsviten nedan; ju fler noder på strängen, desto kortare våglängd och desto högre frekvens.
Kriterier för stående våg
Om strängens längd är och våglängden är så gäller att för att en stående våg ska bildas. är ordningstalet på den stående vågen, och olika värden på ger olika antal noder på den stående vågen.
Stående vågor kan inte enbart bildas på en sträng. De kan även bildas t ex i vatten, på membran och i akustiska musikinstrument (då är det frågan om ljudvåg). Även atomer kan beskrivas matematiskt på ett sätt som inkluderar stående vågor.
Länk till Wikipedias sida om stående vågor
Länk till interaktion i Desmos
Bukar på stående vågor
Beskrivning av buk
Noder på stående vågor
Beskrivning av nod