Etikett: python

Det gyllene snittet är, som kanske bekant, ett förhållande som delar in en sträcka i delsträckorna a och b så att

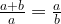
Man kan få fram ett uttryck för det gyllene snittet med hjälp av en andragradsekvation. Det blir ett irrationellt tal som ungefär är 1,618 (det innebär att sträckan a i figuren ovan är 1,618 gånger längre än sträckan b). Men det går även att representera det gyllene snittet med hjälp av ett s.k kedjebråk. Det är ett bråk som består av ett till bråk som är uppbyggt på samma sätt som det första, som i sin tur är uppbyggt av ytterligare ett bråk efter samma mönster osv. Eftersom antalet ”bråk i bråket” går mot oändligheten så går inte annat än att få fram ett närmevärde på det i decimalform. Det är det nedanstående program i Python gör.

Efter 38 iterationer ger programmet 15 korrekta decimaler. Inte det mest effektiva sättet att få fram ett närmevärde på kanske, men ändå kul att ett så pass kort program kan utföra de operationer som snabbt blir bökiga med en vanlig räknare (RPN-räknare undantaget).